Towards Model Predictive Control, Part 2

Implementing MPC

When implementing MPC, we need to be very careful about constraints on dosing insulin.

We made a few changes to the constriants to ensure that: 1. we are not dosing ‘negative’ insulin (i.e., the control action u is always >=0) and 2. that we are not dosing insulin past a control horizon M, which is somewhat shorter than the prediction horizon, T:

constraints += [
    x[:,t+1] == A @ x[:,t] + B @ u[:,t],
    u[:,t] >= 0,
    u[:,t] <= 1.0,
    cp.sum(u[:,:]) <= 5,
    u[:,M:T] == 0
]

With this implementation, at a starting BG of 250 and a target of 100, we arrive at an “optimal control” result that looks like what is shown here: 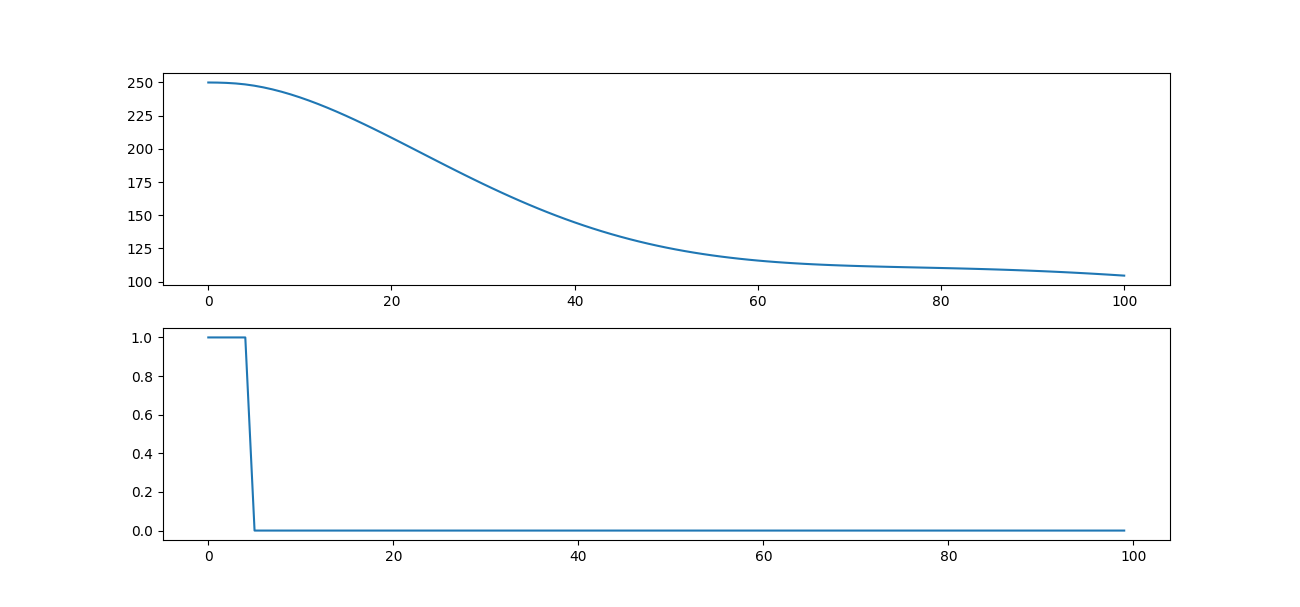The top value is the BG over time, and the bottom value is the control action over time. Of course, the controller will want to “front-load” as much of the insulin as possible – delivering the maximum 1 units of insulin at every timestep until it determines that the final blood glucose value will reach close to the end constraint of the target.

We implement this controller, and… unfortunately, it kills our patients: 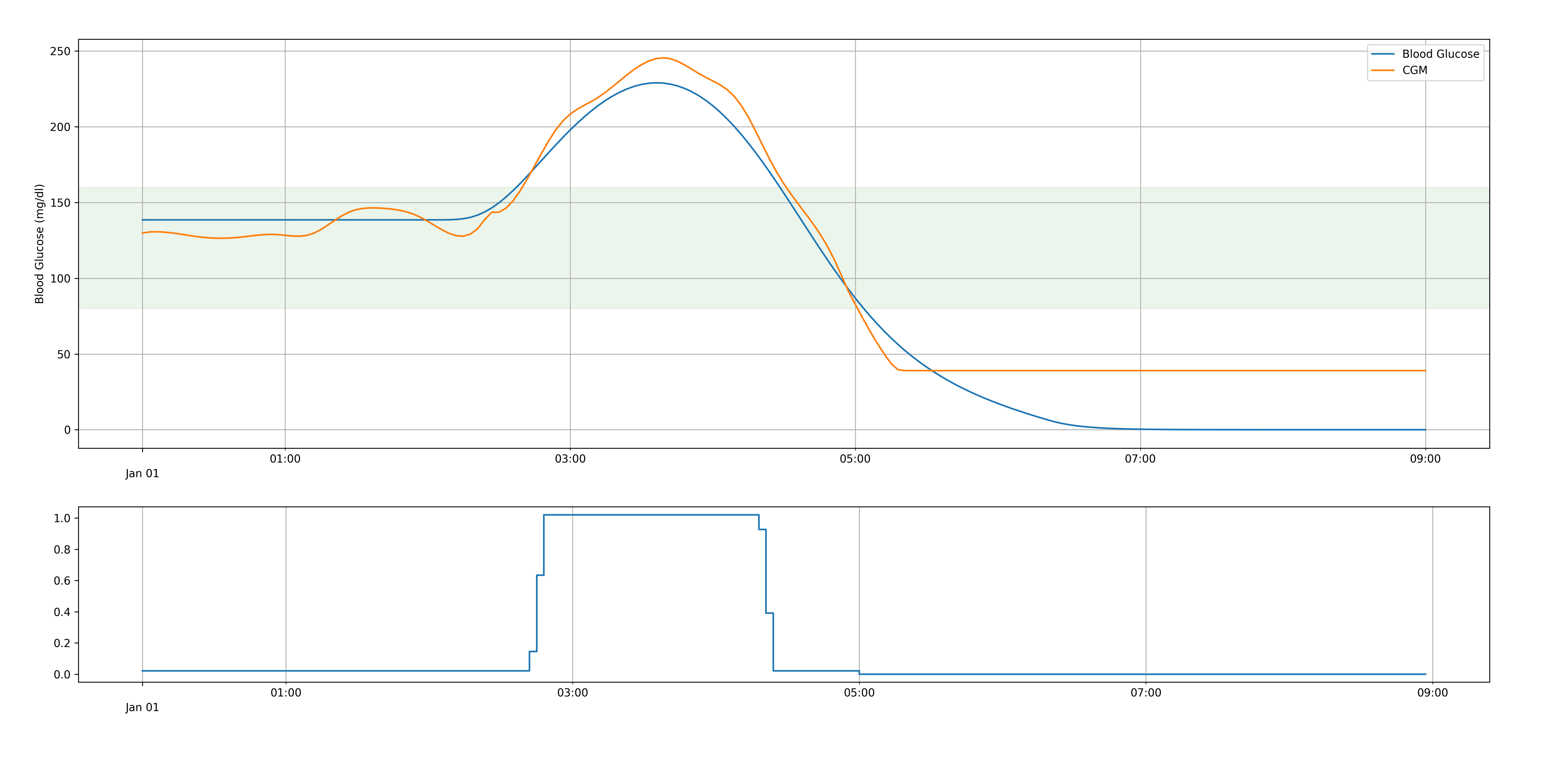Why does this occur?

It happens because we have an incomplete estimate of the state. Under our simple model, The future timestep (a 1x3 vector) depend only on the previous timestep (another 1x3 vector), multiplied by our matrix (a 3x3 matrix), with the effect of future doses of insulin added. This naive estimation of state does not include the prior doses already delivered by the controller, though – this is called the “IOB,” standing for insulin on board, a concept familiar to most diabetics. For our model to accurately determine the effects of future doses of insulin, it must also determine the effects of the insulin that is already delivered.

This can be done in a number of ways. It’s an area we will surely consider if we are to keep our virtual patients alive.

Misc

Also, I implemented a logger. And, as I am working with this codebase, it’s becoming apparent that another rewrite is in order.